扫码预约【1/14上海线下-理工娃早申案例私享会】

“高中阶段培养好奇心”是丘成桐老先生在总决赛颁奖典礼反复提及的一句话。本届丘奖数学的获奖作品则是这段话最好的成果体现。
丘奖是从数学奖“发家”的，今年的数学金奖项目延续了去年的辉煌，再一次摘得了科学金奖，项目水准和个人造诣值得肯定。
不久前我们邀请了有方理科工程学术主管S老师为大家带来了丘奖数学学科专场讲座，期间S老师复盘了丘奖数学总决赛赛况，分享了他对于此赛道的独特观点和对获奖作品的解读评析，下面就一起来回顾一下这场精彩的讲座吧！

本期福利

2023丘奖数学论文扫码添加小师姐回复 丘奖数学 领取

01最全科普！丘奖是什么？
丘成桐中学生科学奖是2008年由数学大师丘成桐先生发起设立的中学生科学创新类奖项，是以“科研学术论文”和“专业学术答辩”为评价主体的科学赛事，倡导创新思维和团队合作，舍弃试卷和标准答案，以提交论文的形式参赛。
丘成桐中学科学奖从十五年前单一的数学奖，发展到今天的数学奖、物理奖、化学奖、生物奖、计算机奖和经济金融建模奖，并入选2022-2025学年教育部赛事白名单，在国内外都具有极高的影响力。
官网：http://www.yau-awards.com/
丘奖三大赛区划分
中国内地赛区
中国内地各大中学的在校学生（仅限高中生），各学科分南、北部评审，数学奖还设有东部赛区
亚洲赛区
除中国内地外，港澳台地区及亚洲其他国家的中学生
北美赛区
除亚洲国家外，其他海外国家的中学生
如果你有幸进入丘奖的决赛并拿奖，就有机会获得丘成桐先生亲自撰写的推荐信。即便没有获奖，这份完整的科研经历及论文成果，也能在申请中成为你不可或缺的点睛之笔。丘奖年年吸引不少青少年参加的原因有以下两点：
01 具有国际影响力
截至目前，丘奖已成功举办十五届，累计超过2000余所中学、12000余支队伍参赛，覆盖国内30余个省市自治区和美国、新加坡等多个海外国家，共461余个学生团队的近850余人受到奖励，450余位全球各国的知名教授、科学家担任奖项的评委或顾问。
02 成功助力申请
超过1/2的获奖中学生经推荐分别进入清华、北大、哈佛、MIT、耶鲁和普林斯顿等中外知名大学就读，其中不乏进入理想大学后依然坚持学术研究的科研人才。

02丘奖数学评审标准
随着数学参赛作品质量不断提升，赛道越来越“卷”，学科的评审也越发严格。S老师把近年来的数学赛道评审要素总结为以下5点：
评审标准总结：
1.与数学学科的相关性（纯数学和应用数学，统计学和概率）
2. 研究思路（研究主题选择）和/或者研究构思（研究方法选择）的原创性
3.问题解决和方法学方面的创造性
4.数学推导方面的严密性
5.对未来数学发展的潜值
好的开头就成功了一半，一个适合丘奖的选题更能让参赛者如虎添翼。而对于学生来说，除了关注自己的选题，研究方法也需要格外注意，其结果都要能最大化实现理论和方法上的创新。
03丘奖数学获奖作品解读
在今年数学获奖作品里，大部分的项目都运用到了建模的手段，和计算机学科类似，很多贴近生活的项目都非常吃香。
首先我们先看看拿下今年数学金奖暨科学金奖的获奖作品：
学生提出了简短而快速的DIT或dDIT解决方案，几乎可以立即解决问题，论文中汇编了更重要的此类实例，每一个实例都证明了这一强大定理的更广泛应用。此外，该项目还发现了DIT和dDIT可以用来证明几何中的许多其他定理，并用于进一步扩展它们的证明。
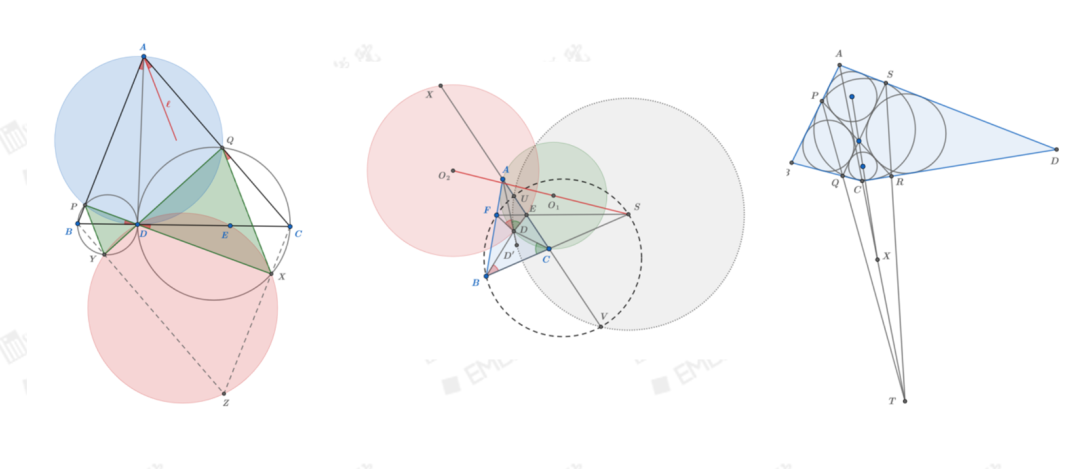项目中有一点非常出众：文中提出的所有解决方案都设法完全避开了二次曲线的使用，证明了一个事实，即通常与DIT的学习和应用相关联的二次曲线的概念根本没有必要。最后，该项目做了这个定理的一个有趣的应用类型：the imaginary realities，它是Desargues对合定理的一个漂亮的概念和扩展。
我们可以看到该同学对Desargues对合定理及其对偶在解题和证明其他定理方面的能力，以及对原定理的各种扩展的深入探索。结合她在颁奖典礼上的发言我们能够看到她对数学怀有崇敬、热情、好奇，这种发自内心的热爱会让她在数学这条学术之路上走得更远。

纵览今年的数学获奖作品，以下两个创新项目也吸引到了我们的注意。
往年数学的很多课题都是纯数，这个课题是利用了数学建模。但这个模型并不是学生自己所建，而是运用了成熟的中型企业模型建立微分方程组，使用加权齐次多项式和特征曲线，得到两类不变代数曲面。
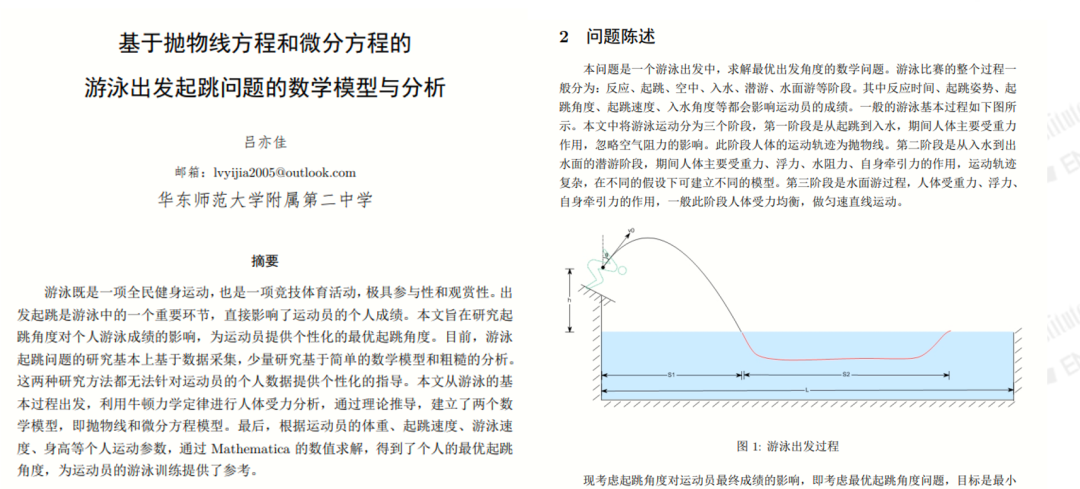这个项目的作者自身是一名跳水运动员，他以游泳发出起跳作为研究点，试图建立抛物线和微分方程模型来找到一个最佳的跳水角度，从而达到非常好的入水状态。这个项目非常符合我们对建模的想象，同时这个课题也是和物理非常相关的数学课题。

04如何找到一个感兴趣的研究问题
对于中学生来说，想要进行一个完整的科研，兴趣是非常是重要的，因此如何找到一个自己感兴趣的研究问题作为中学生开始科研的第一步来说就非常关键。
根据有方多年为学生一对一定制科研规划的经验，以下三个问题对于学生开启一段科研经历来说非常关键：
1你想做一个什么样的研究？
是否已经深入了解过了一些更高阶或者复杂的数学内容？
如果有，你是否有一些自己感兴趣的数学分支？
如果没有，你比较擅长数学的什么方面？
2研究内容确定后，如何完成课题？
不需要所有的数学分支内容都完全掌握，针对课题能够掌握即可
探寻可行的要研究问题的解决办法
3了解过要研究问题后，你准备好了吗？
根据自身的知识水平和能力客观评估项目
妥善安排项目周期，定时复盘
想要让孩子通过科研项目来助力梦校申请，项目的选择、时间管理和良好的心态都是成败的关键要素。做科研切记左右开工，要强调一致性与延伸性，以兴趣为出发点，自我驱动力的加持会让科研更加事半功倍！

扫码回复【0103】预约 ↓

如果想要早一步获取免费作品集福利，快快扫码添加小师姐备注【孩子就读地区＋年级】，讲座结束后第一时间为您安排福利的发放！